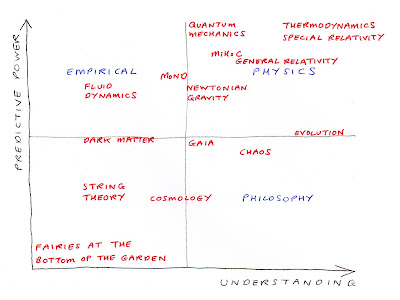
The problem with mainstream theoretical physics today is a lack of connection to reality. String theory or loop quantum gravity, for example, are like constructed virtual realities that bear no direct relation to the real world. The proof is that neither of the theories are testable: they cannot be disproven, and this has given them a longevity they do not deserve.
There is a related trend in modern art and this is interesting because both art and science are ways of modelling the world. In a similar way, art used to be testable. An artist draws a face or and lanscape and there is an objective test. Does it look like the real thing? If so, we can say that the artist has skill. Then the camera came along and this skill became obsolete. Art reappeared in a form detached from reality: abstract art. I won't attempt to judge modern art, but a science detached from reality is a disaster, and takes us back before Empiricism and Roger Bacon!
String theorists may say it is not their fault that the theory cannot be tested. But it IS their fault. If they are scientists they need to work on theories that are testable. Either devise a test or forget the theory and start looking at the real world. This used to be the first rule of science, but it has been allowed to lapse. It reminds me of a comment I once read about ancient Greek science when it had passed its peak and humanity was heading for the dark ages: "Speculation ran way beyond the testable and dwindled into metaphysics" (McEvedy, 1961). I hope we are not drifting into a dark age where smug scholars in ivory towers discuss uselessly what came before the big bang, when they can't explain how local galaxies behaved last week, or even why the turbulence in a pipe starts when it does. The best progress has always come from a little thought applied to interesting observations: a prism experiment lead to a better theory of light, a view of Jupiter's orbiting moons through a telescope inspired heliocentricity and gravity, and the null result from the Michelson-Morley experiment lead to relativity.
On a positive note, I worked for ten years at the UK Met Office, in the ocean forecasting section (not climate research) and the ethos in this Ocean Forecasting section and also in the NWP (Numerical Weather Prediction) was healthy, because the ocean or atmosphere models had to forecast data that was continually coming in from satellites, weather stations and ocean buoys in the real world, so there was a constant check from reality to test and improve the models. This is the best way to do science: lots of data, some anomalies, and a little thinking applied.
I'll leave the last word to Sherlock Holmes' creator: "It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts." - Sir Arthur Conan Doyle.
McEvedy, C., 1961. The Penguin Atlas of Ancient History. Penguin Books. (Page 92).